这个博客用来回忆这道题目,本人算法新手
题目:
在给定的 m x n 网格 grid 中,每个单元格可以有以下三个值之一:
- 值
0 代表空单元格;
- 值
1 代表新鲜橘子;
- 值
2 代表腐烂的橘子。
每分钟,腐烂的橘子 周围 4 个方向上相邻 的新鲜橘子都会腐烂。
返回 直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能,返回 -1 。
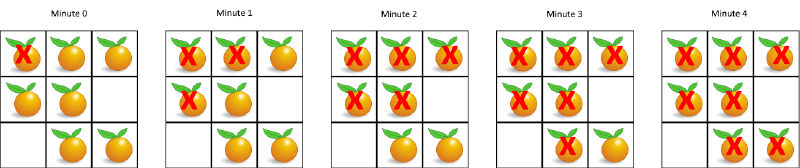
- 示例 1:

输入:grid = [[2,1,1],[1,1,0],[0,1,1]]
输出:4
输入:grid = [[2,1,1],[0,1,1],[1,0,1]]
输出:-1
解释:左下角的橘子(第 2 行, 第 0 列)永远不会腐烂,因为腐烂只会发生在 4 个方向上。
输入:grid = [[0,2]]
输出:0
解释:因为 0 分钟时已经没有新鲜橘子了,所以答案就是 0 。
提示:
m == grid.lengthn == grid[i].length1 <= m, n <= 10
grid[i][j] 仅为 0、1 或 2
解题思路
- 先遍历所有的网格,统计新鲜橘子的个数,并把腐烂的橘子添加到队列。
- 使用广度优先搜索(BFS),不断感染四周的橘子,将已经感染过其他橘子的烂橘子从队列中弹出(便于统计还有哪些橘子没有感染其他好橘子)。每感染一个橘子,将新鲜橘子个数减去一。每感染一轮,时间加一。
- 最后检测新鲜的橘子个数是否为零,如果为零,则返回总共花去的分钟数;如果新鲜的橘子个数不为零,说明还有橘子永远不会被感染,根据题目要求,返回
-1。
解题代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
class Solution {
public:
int orangesRotting(vector<vector<int>>& grid) {
int m = grid.size(); //记录每一行的橘子个数
if (m == 0) return -1; //如果没有橘子,直接返回-1
int n = grid[0].size(); //记录每一列橘子个数
if (n == 0) return -1;
queue<pair<int, int>> q;
int fresh = 0;
//遍历所有网格
for (int i = 0; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (grid[i][j] == 1) { //如果为新鲜橘子
fresh++; //新鲜橘子个数就加一
}
if (grid[i][j] == 2) { //如果橘子不是新鲜的
q.emplace(i, j); //就把烂橘子放入队列
}
}
}
//开始广度优先搜索(BFS)
int minutes = 0;
vector<pair<int, int>> dirs = { {1,0},{-1,0},{0,1},{0,-1} }; //定义四个方向
while (!q.empty() && fresh > 0) { //如果队列q不为空且有新鲜橘子
int size = q.size(); //记录才开始或几轮下来还有多少未感染其他橘子的烂橘子
for (int k = 0; k < size; ++k) { //对这些橘子进行遍历
auto [i, j] = q.front(); //获取队列中第一个未感染其它橘子的烂橘子
q.pop(); //将该橘子弹出
for (const auto& [x, y] : dirs) { //遍历四个方向
int dx = i + x, dy = j + y; //计算烂橘子四周的坐标值
if (dx >= 0 && dx < m && dy >= 0 && dy < n && grid[dx][dy] == 1) { //如果在矩阵范围内且该橘子是好橘子(避免重复感染和越界问题)
grid[dx][dy] = 2; //就感染这个橘子
q.emplace(dx, dy); //将这个橘子添加到未感染其它橘子的烂橘子的队列
fresh--; //好橘子数量就减一
}
}
}
++minutes; //计算时间
}
return fresh == 0 ? minutes : -1;
}
};
|
提交结果