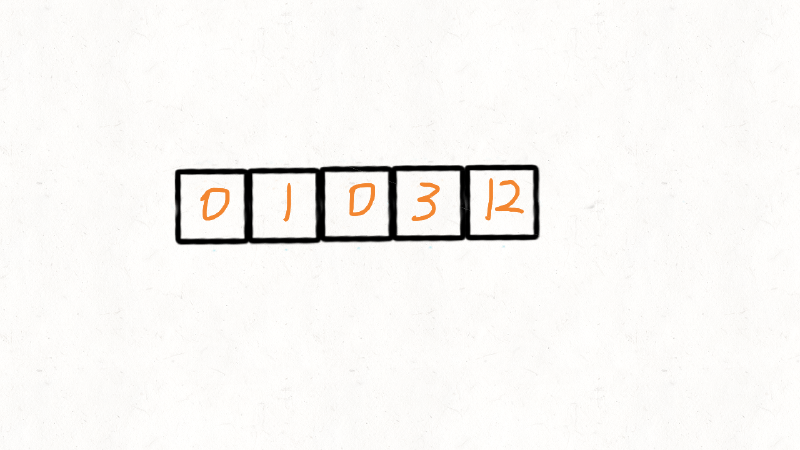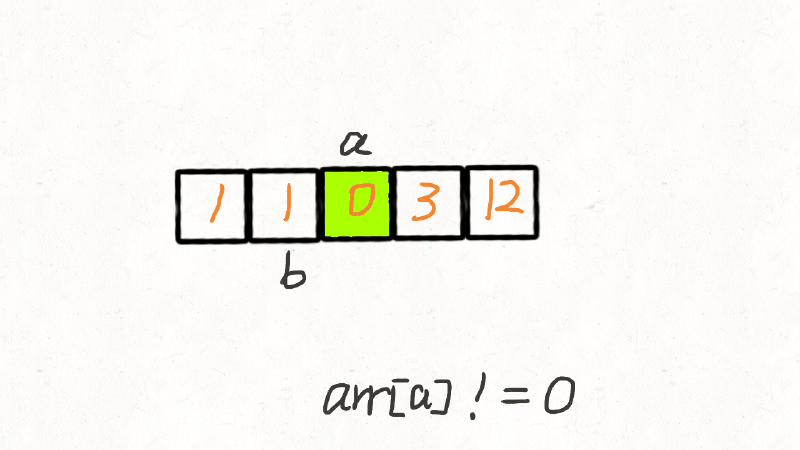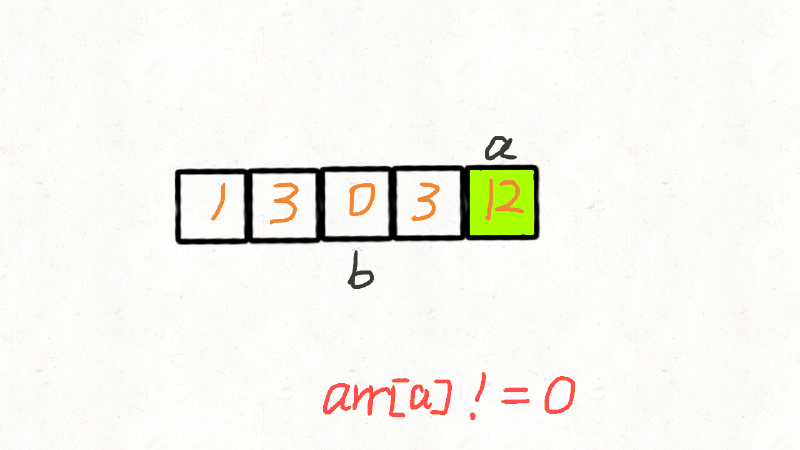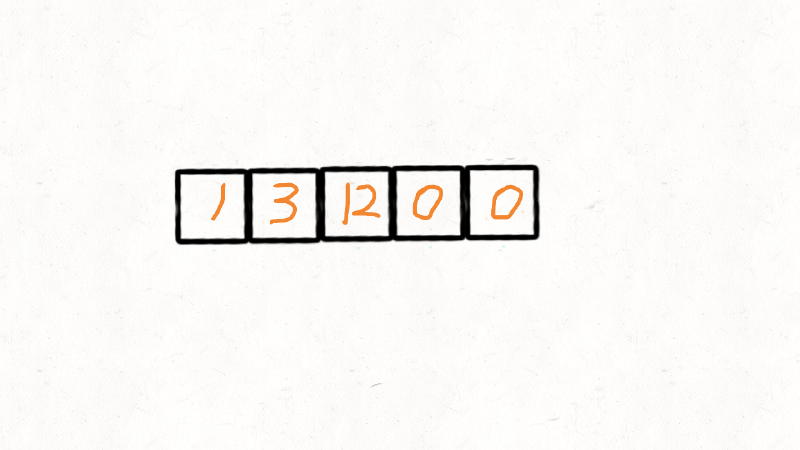LeetCode 第283题移动零

题目：

给定一个数组 nums，编写一个函数将所有 0 移动到数组的末尾，同时保持非零元素的相对顺序。

请注意 ，必须在不复制数组的情况下原地对数组进行操作。

示例 1:

输入: nums = [0,1,0,3,12]

输出: [1,3,12,0,0]

示例 2:

输入: nums = [0]

输出: [0]

提示:

$1 <= nums.length <= 104$
$-231 <= nums[i] <= 231 - 1$

解法一：二次遍历

思路：

第一个指针用来遍历数组，另外一个指针位于上次与第一个指针指向的数交换的位置。

大致原理：

一个指针A指向索引为0的位置，另一个指针B从头开始遍历。每当指针B遇到一个非零数，都要把这个数依次从这个数组从头部往后放。从而保证非零数连续的在这个数组前面。然后其它部分填上0。

主要过程：

指针B 用来遍历数组。
每当遇到非零元素时，指针A 就把它放到当前的位置，并移动到下一个空位置。
最终，指针A会停在数组中的最后一个非零数的位置，而指针B会遍历整个数组。
数组中剩下的部分自动是零，因为非零元素已经被移到了前面。

动画演示（来源于网络）：

动画演示

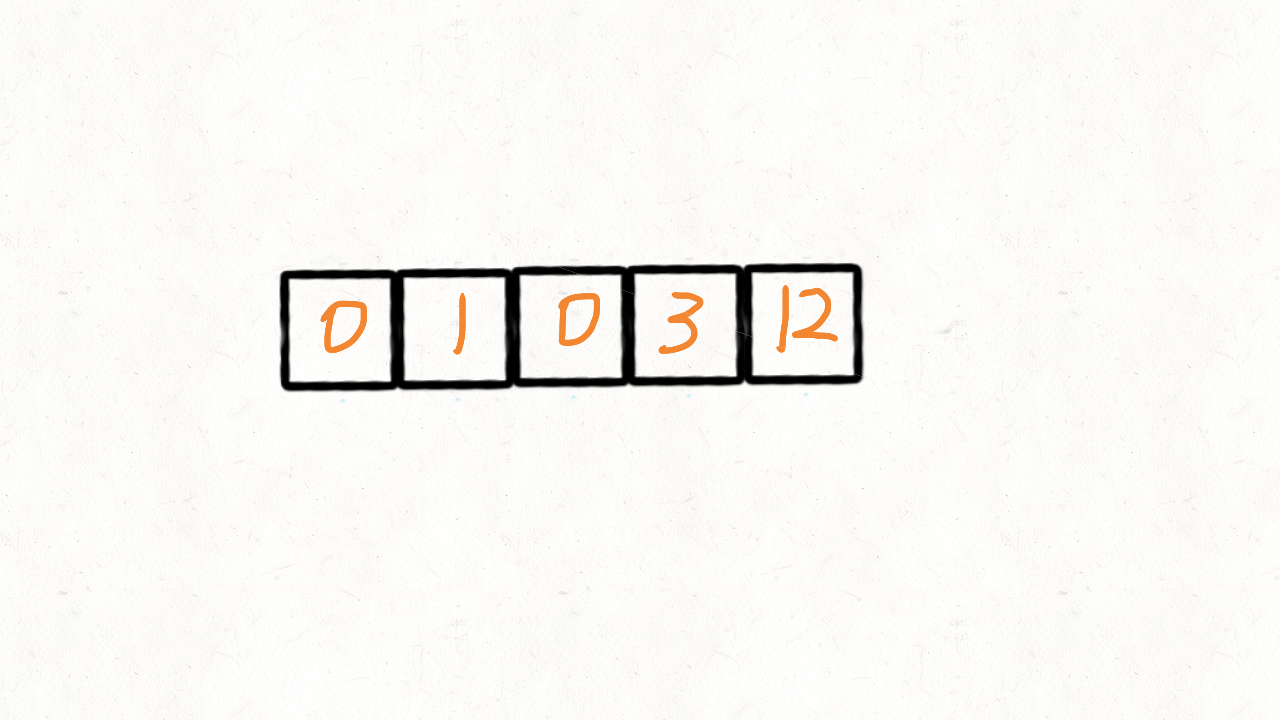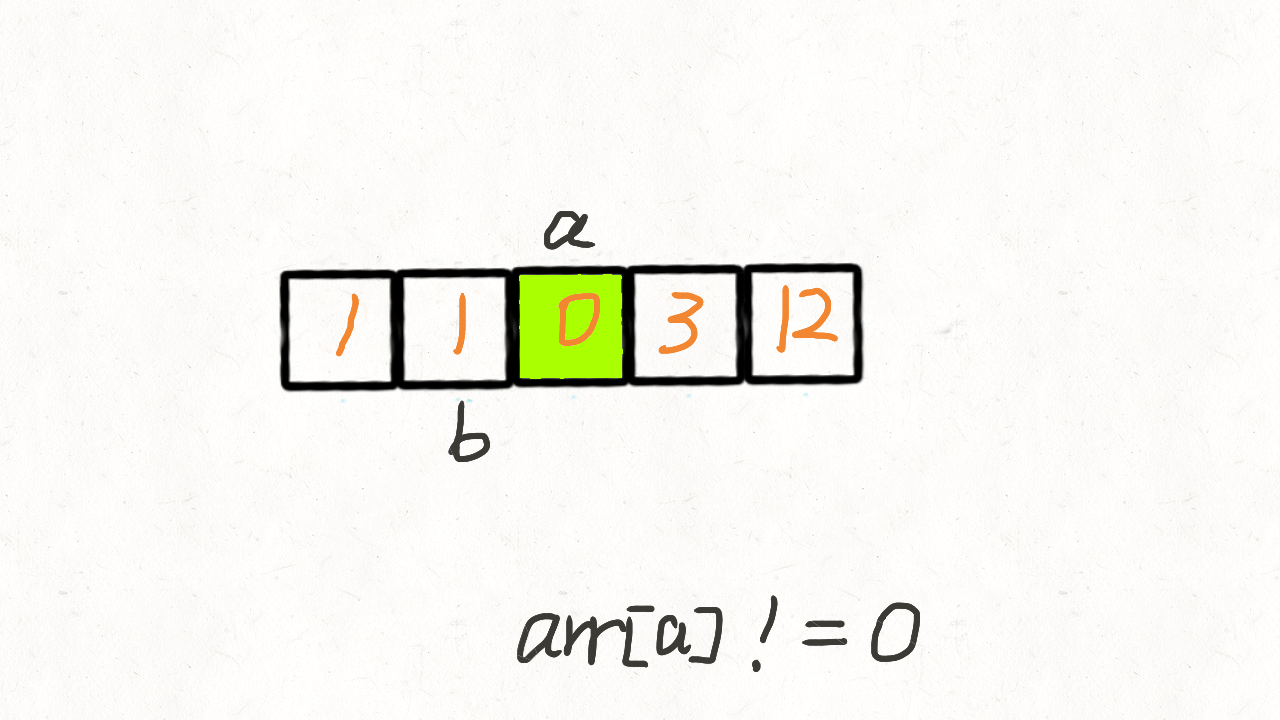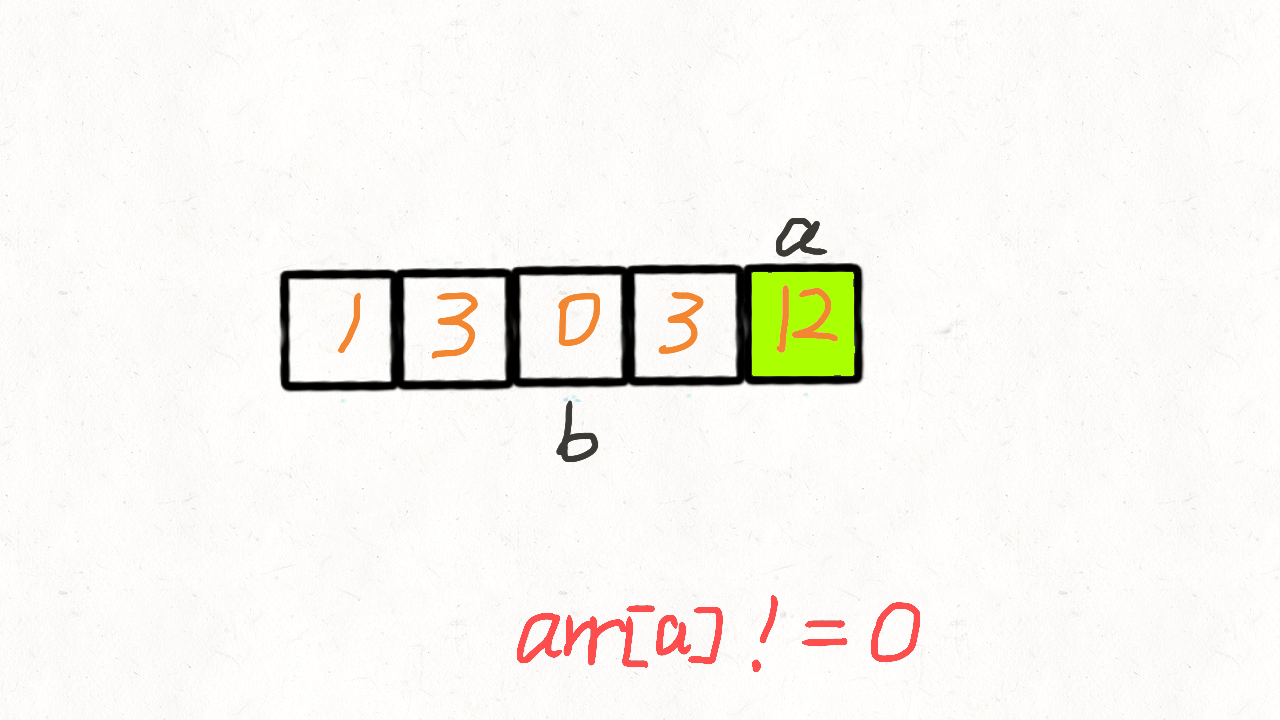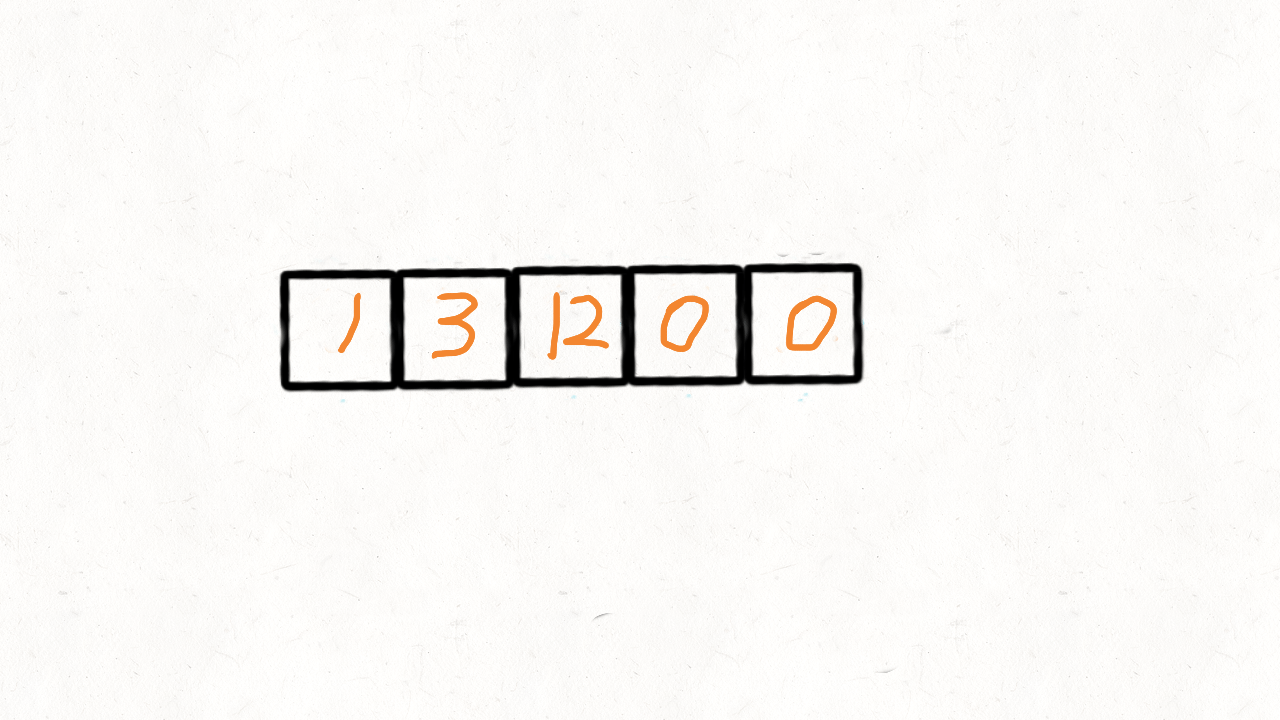
解题代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


class Solution {
    public void moveZeroes(int[] nums) {
        int insertPos = 0;
        for (int i = 0; i < nums.length; i++) {
            if (nums[i] != 0) {
                nums[insertPos++] = nums[i];     //把非零元素放到当前的前面
            }
        }
        for (int i = insertPos; i < nums.length; i++) {
            nums[i] = 0;    //其余部分补上0
        }
    }
}

复杂度：

时间复杂度：$O(n)$
空间复杂度：$O(1)$

解法二：交换法（官方给出的解法）

大致原理：

左指针指向上一次交换的位置，右指针遍历数组，当遇到不为零的数，就与左指针指向的数交换位置，总体上会把为零的数不断向右赶。

左指针左边均为非零数；

右指针左边直到左指针处均为零。

因此每次交换，都是将左指针的零与右指针的非零数交换，且非零数的相对顺序并未改变。

解题代码：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


class Solution {
    public void moveZeroes(int[] nums) {
        int left = 0;
        for (int right = 0; right < nums.length; right++) {
            if (nums[right] != 0) {
                swap(nums, right, left);
                left++;
            }
        }
    }

    public void swap(int[] nums, int left, int right) {
        int temp = nums[left];
        nums[left] = nums[right];
        nums[right] = temp;
    }
}

复杂度：

时间复杂度：$O(n)$
空间复杂度：$O(1)$

两者的优缺点分析：

第一种“二次遍历“方法直接赋值操作，节省了开销，但是需要二次遍历，可能会对性能产生影响。
第二种”交换法“无需二次遍历，但是交换操作在某些情况下可能会达到性能瓶颈。